Die Dauer der Methode ist kürzer und die Justierung auf einen neuen Messpunkt schneller. Dieses neue Röntgendiffrakometer wird in Japan unter dem Namen pulstec μ-X360s hergestellt. Es handelt sich um die zweite Generation dieses Geräts, das seit mehr als acht Jahren auf dem Markt ist.

Beschreibung der Cos-α-Methode
Der theoretische Hintergrund der Cos-α-Methode wird hier nicht behandelt. Sie können ihn in den folgenden Referenzen nachlesen [1, 2, 3]. Eine ausführliche Zusammenfassung der gesamten Methode mit ihren Möglichkeiten ist in [4] dargestellt. In diesem Artikel wird eine praktische Beschreibung gegeben. Die Methode basiert auf einem Debye-Scherrer-Ring. Röntgenstrahlen wurden auf die Oberfläche der zu messenden Probe gerichtet. Aufgrund des Braggschen Gesetzes werden die einfallenden Röntgenstrahlen unter einem ganz bestimmten Winkel reflektiert, der vom Atomabstand im Material abhängt. Einzelheiten zur Braggschen Reflexion findet man z. B. in [5, 6]. Aufgrund der unterschiedlichen Ausrichtung der Atomschichten in polykritallinen Materialien, in diesem Fall Körner des Federstahls, wird ein vollständiger Ring reflektiert.

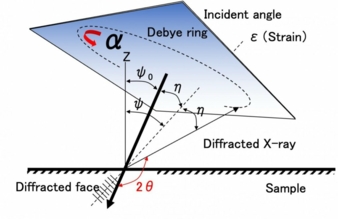
Das Röntgendiffraktometer strahlt unter einem bestimmten Einfallswinkel zur Oberfläche (in diesem Fall 35° für Martensit) Röntgenstrahlen aus. Der Einfallswinkel bestimmt die Richtung der gemessenen Atomschichten. Ein vollständiger Ring wird, wie in Abbildung 1 dargestellt, reflektiert. Der gesamte Ring wird von einem Flächendetektor erfasst. [7]. Der reflektiere Ring geht sowohl in Vorwärtsrichtung als auch als Rückstreuung (back scattering) wie in Abbildung 1 dargestellt.

Abbildung 1: Schema des Debye-Scherrer-Rings und die benutzten Parameter.

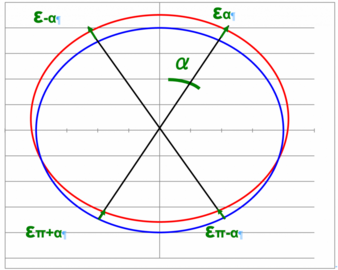
Der Debye-Scherrer-Ring hat sich ein wenig in Messrichtung verschoben, wenn in der Probe Restspannungen vorhanden sind. Druckspannung verringert den Atomabstand, Zugspannung vergrößert ihn. Dadurch ändert sich der Rückstreuwinkel 2 Θ. Die Situation ist in Abbildung 2 dargestellt. Der rote Ring steht beispielsweise für die Reflexion ohne Spannung, der blaue für die Reflexion mit Spannung dar.

Abbildung 2: Verschiebung der Debye-Scherrer-Ringe unter Belastung der Probe.

Die Verschiebung εα1 des Ringes unter einem bestimmten Winkel α ist definiert als:

Die Verschiebung ist proportional zu cos α:

(Die einzelnen Größen sind Abbildung 1 zu entnehmen.)

Aus der Steigung kann die Restspannung mit Hilfe des E-Moduls und der Poissonzahl ermittelt werden, da der Atom- oder Gitterebenenabstand proportional zur makroskopischen Dehnung ist. Alle anderen Faktoren sind konstant.

Experimenteller Aufbau
Die Anordnung ist in Abbildung 3 zu sehen. Dargestellt ist das gesamte Diffraktometer pulstec μ-X360s ohne Netzteil. Es ist etwa 35 cm lang. In diesem Fall wird es sehr häufig zur Bestimmung von kugelgestrahlten Federn verwendet. Daher stellt sich die Frage, ob es die gleichen Ergebnisse liefert wie die traditionelle sin2Ψ-2Θ-Methode (sin2Ψ-2Θ-Methode, siehe z. B. Bob. B. He: Two-Dimensional X-Ray Diffraction [8]).

Es wurde eine spannungsgestrahlte Blattfederprobe verwendet und mit den beiden Methoden ein Eigenspannungsprofil in der Tiefe bestimmt. Die Zugfestigkeit Rm der Probe betrug Rm = 1700 MPa. Das Material war 50 CrV 4 (1.1859). Um die Eigenspannungen in der Tiefe zu messen, wurde das darüber liegende Material in einem Bereich von 8 mm Durchmesser elektrolytisch entfernt. Als zweites Gerät wurde ein Strainflex MSF-2M der Firma Rigaku verwendet. Es wurde in beiden Fällen Cr-Kα-Strahlung verwendet. Daraus ergibt sich die Gitterebene [2,1,1]. Die Messfleckgröße betrug 6 * 8 mm (Rigaku) bzw. war 4 mm Durchmesser (pulstec). Das Rigaku-Gerät wurde als Ω-Goniometer benutzt. Es wurde mit mindestens vier Einstrahlwinkeln gemessen.

Abbildung 3: Das Röntgendiffraktometer µ-X360s (pulstec) mit der Blattfederprobe.

In Abbildung 4 sind die Messergebnisse dargestellt. Es wurde bis auf eine Tiefe von 650 µm gemessen. Darüber hinaus werden die Werte recht ungenau, da sich die Lochgeometrie anfängt stärker zu verändern. Die Unterschiede zwischen den beiden Kurven sind Messfehler (statistisch wie systematisch), die bei beiden Methoden etwa 7 % betragen. Beide Eigenspannungsverteilungen sind innerhalb der Fehlergrenzen kompatibel.

Abbildung 4: Eigenspannungsverteilungen in Abhängigkeit von der Tiefe.

Zusammenfassung
Beide Methoden liefern für Federstahl die gleichen Ergebnisse. Das bedeutet, dass die Cos-α-Methode hervorragend zur Bestimmung von (Eigen-)spannungen in Federn geeignet ist. Auch für andere Materialien wurde diese Übereinstimmung festgestellt [9,10 und Referenzen dort]. Diese Methode wird zunehmend eingesetzt und eignet sich auch für andere Federelemente. Der minimale Drahtdurchmesser sollte bei mindestens bei 2 mm liegen. Der Messfleck kann auf eine minimale Größe von 400 µm Durchmesser (von 4 mm ausgehend) reduziert werden. Auf der anderen Seite kann in vielen Bereichen auch außerhalb des Labors an Großbauteilen (z. B. Walzen, Eisenbahnrädern oder Brücken) die Methode benutzt werden. Natürlich ist sie auch für Draht geeignet, um z. B. Ziehspannungen festzustellen.

Literatur
[1| K. Tanaka, Y. Akiniwa: Diffraction Measurements of Residual Macrostress and Microstress Using X-Rays, Synchrotron and Neutrons, JSME International Journal Series A, 47 (2004), S. 252- 263
[2] J. Ramirez-Rico, S.-Y. Lee, J. J. Ling, I. C. Noyan: Stress measurement using area detectors: a theoretical and experimental comparison of different methods in ferritic steel using a portable X-ray apparatus, Journal of Materials Science 51 (2016), S. 5343–5355
[3] T. Sasaki: New Generation X-Ray Stress Measurement Using Debye Ring Image Data by Two-Dimensional Detection, Materials Science Forum Vol. 783-786 (2014), S. 2103-2108
[4] E. Müller, J. Behler: Determination of Residual Stress by X-Ray Diffraction with the Cos-Alpha Method and Its Application, in Gül?en Ak?n Evingür and Önder Pekcan (Hrsg): Residual Stress Measurements Intechopen, 2024, DOI: 10.5772/intechopen.1003795
[5] H. Linder: Physik für Ingenieure, Fachbuchverlag Leipzig, München, 2014, S. 698
[6] D. C. Giancoli: Physik, Pearson, Hallbergmoos, 2018, S. 1206
[7] E. Müller: The Debye–Scherrer technique – rapid detection for applications. Open Physics, Open Physics, vol. 20, no. 1, 2022, S. 888-890. https://doi.org/10.1515/phys-2022-0193
[8| B. B. He: Two-Dimensional X-Ray Diffraction, John Wiley and Sons Inc., Hoboken, 2009, S. 263
[9] D. Delbergue, D. Texier, M. Lévesque, P. Bocher: Comparison of Two X-Ray Residual Stress Measurement Methods: Sin 2 ψ and Cos α, Through the Determination of a Martensitic Steel X-Ray Elastic Constant, Materials Research Proceedings 2 (2016) S. 55-60
[10] E. Müller: The long-term stability of residual stresses in steel, S/N Applied Sciences, (2021) 3:877, https://doi.org/10.1007/s42452-021-04867-z

Der Autor des Beitrags ist Eckehard Müller, Steinbeis-Transferzentrum für Federntechnologie, Bauteileverhalten und Prozess.

Steinbeis-Transferzentrum für Federntechnologie,
Bauteileverhalten und Prozess
Langerfeldstraße 53c
58638 Iserlohn
Ansprechpartner ist Eckehard Müller
Tel.: +49 171 1245298
eckehard.mueller@hs-bochum.de
www.metallfedern.eu